How Do You Know When to Use Conservation of Angular Momentum

Chapter 10 Rotational Motion and Athwart Momentum

10.v Angular Momentum and Its Conservation

Summary

• Understand the analogy between angular momentum and linear momentum.
• Detect the relationship between torque and athwart momentum.
• Employ the police of conservation of athwart momentum.

Why does World proceed on spinning? What started it spinning to begin with? And how does an ice skater manage to spin faster and faster simply by pulling her arms in? Why does she non have to exert a torque to spin faster? Questions like these accept answers based in angular momentum, the rotational analog to linear momentum.

By now the blueprint is clear—every rotational phenomenon has a direct translational analog. It seems quite reasonable, then, to define angular momentum [latex]{L}[/latex] equally

[latex]{L=I\omega}.[/latex]

This equation is an analog to the definition of linear momentum as [latex]{p=mv}.[/latex] Units for linear momentum are [latex]{\text{kg}\cdotp\text{m/southward}}[/latex] while units for angular momentum are [latex]{\text{kg}\cdotp\text{yard}^2\text{/s}}.[/latex] As we would wait, an object that has a large moment of inertia [latex]{I},[/latex] such equally Earth, has a very big athwart momentum. An object that has a big angular velocity [latex]{\omega},[/latex] such as a centrifuge, also has a rather large athwart momentum.

MAKING CONNECTIONS

Angular momentum is completely analogous to linear momentum, first presented in Chapter 6 Uniform Circular Motion and Gravitation. It has the same implications in terms of conveying rotation forward, and it is conserved when the net external torque is zilch. Angular momentum, like linear momentum, is also a holding of the atoms and subatomic particles.

Example 1: Calculating Angular Momentum of the World

Strategy

No information is given in the statement of the problem; so we must look upwardly pertinent data before we tin calculate [latex]{L=I\omega}.[/latex] Outset, co-ordinate to Affiliate 10.iii Making Connections, the formula for the moment of inertia of a sphere is

[latex]{I\:=}[/latex] [latex]{\frac{2MR^two}{5}}[/latex]

and so that

[latex]{L=I\omega=}[/latex] [latex]{\frac{2MR^2\omega}{v}}.[/latex]

Earth's mass [latex]{K}[/latex] is [latex]{5.979\times10^{24}\text{ kg}}[/latex] and its radius [latex]{R}[/latex] is [latex]{6.376\times10^six\text{m}}.[/latex] The Earth'southward angular velocity [latex]{\omega}[/latex] is, of form, exactly 1 revolution per solar day, but we must covert [latex]{\omega}[/latex] to radians per second to do the adding in SI units.

Solution

Substituting known information into the expression for [latex]{L}[/latex] and converting [latex]{\omega}[/latex] to radians per second gives

[latex]\begin{assortment}{lcl} {L} & {=} & {0.four(5.979\times10^{24}\text{ kg})(half-dozen.376\times10^6\text{ grand})^two(\frac{ane\text{ rev}}{d})} \\ {} & {=} & {nine.72\times10^{37}\text{ kg}\cdotp\text{m}^two\cdotp\text{rev/d.}} \end{array}[/latex]

Substituting [latex]{2\pi}[/latex] rad for [latex]{1}[/latex] rev and [latex]{8.64\times10^four\text{ s}}[/latex] for one twenty-four hour period gives

[latex]\begin{array}{lcl} {50} & {=} & {(9.72\times10^{37}\text{ kg}\cdotp\text{m}^2)(\frac{ii\pi\text{ rad/rev}}{viii.64\times10^4\text{ south/d}})(1\text{ rev/d})} \\ {} & {=} & {seven.07\times10^{33}\text{ kg}\cdotp\text{yard}^2\textbf{/s.}} \terminate{array}[/latex]

Discussion

This number is large, demonstrating that Earth, as expected, has a tremendous angular momentum. The answer is approximate, because we accept assumed a constant density for Earth in order to estimate its moment of inertia.

When you button a merry-go-circular, spin a bike wheel, or open a door, yous exert a torque. If the torque you lot exert is greater than opposing torques, and then the rotation accelerates, and angular momentum increases. The greater the internet torque, the more rapid the increase in [latex]{L}.[/latex] The relationship betwixt torque and angular momentum is

[latex]{\text{net }\tau\:=}[/latex] [latex]{\frac{\Delta{50}}{\Delta{t}}.}[/latex]

This expression is exactly coordinating to the relationship between strength and linear momentum, [latex]{F=\Delta{p}/\Delta{t}}.[/latex] The equation [latex]{\text{net }\tau=\frac{\Delta{L}}{\Delta{t}}}[/latex] is very fundamental and broadly applicable. It is, in fact, the rotational grade of Newton'due south second law.

Example ii: Calculating the Torque Putting Angular Momentum Into a Lazy Susan

Figure ane shows a Lazy Susan nutrient tray being rotated by a person in quest of sustenance. Suppose the person exerts a 2.l N force perpendicular to the lazy Susan'south 0.260-k radius for 0.150 s. (a) What is the terminal athwart momentum of the lazy Susan if information technology starts from rest, assuming friction is negligible? (b) What is the last angular velocity of the lazy Susan, given that its mass is 4.00 kg and bold its moment of inertia is that of a disk?

Figure ane. A partygoer exerts a torque on a lazy Susan to make information technology rotate. The equation cyberspace τ=ΔFifty/Δt gives the relationship betwixt torque and the athwart momentum produced.

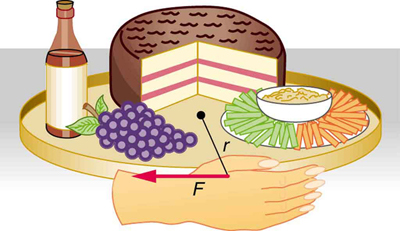
Strategy

We tin find the angular momentum by solving [latex]{\text{net }\tau=\frac{\Delta{L}}{\Delta{t}}}[/latex] for [latex]{\Delta{L}},[/latex] and using the given information to calculate the torque. The concluding angular momentum equals the change in angular momentum, because the lazy Susan starts from residuum. That is, [latex]{\Delta{L}=L}.[/latex] To observe the last velocity, we must calculate [latex]{\omega}[/latex] from the definition of [latex]{50}[/latex] in [latex]{L=I\omega}.[/latex]

Solution for (a)

Solving [latex]{\text{net }\tau=\frac{\Delta{L}}{\Delta{t}}}[/latex] for [latex]{\Delta{Fifty}}[/latex] gives

[latex]{\Delta{L}=\text{net }\tau\Delta{t}}.[/latex]

Because the force is perpendicular to [latex]{r},[/latex] we meet that [latex]{\text{internet }\tau=rF},[/latex] so that

[latex]\brainstorm{assortment}{lcl} {L} & {=} & {\text{rF}\Delta{t}=(0.260\text{ m})(two.50\text{ North})(0.150\text{ s})} \\ {} & {=} & {ix.75\times10^{-2}\text{ kg}\cdotp\text{m}^two\textbf{/s.}} \finish{array}[/latex]

Solution for (b)

The last angular velocity can exist calculated from the definition of angular momentum,

[latex]{Fifty=I\omega.}[/latex]

Solving for [latex]{\omega}[/latex] and substituting the formula for the moment of inertia of a disk into the resulting equation gives

[latex]{\omega\:=}[/latex] [latex]{\frac{L}{I}}[/latex] [latex]{=}[/latex] [latex]{\frac{L}{\frac{one}{2}MR^2}}.[/latex]

And substituting known values into the preceding equation yields

[latex]{\omega\:=}[/latex] [latex]{\frac{nine.75\times10^{-2}\text{ kg}\cdot\text{m}^ii\text{/due south}}{(0.500)(4.00\text{ kg})(0.260\text{ m})}}[/latex] [latex]{=0.721\text{ rad/s.}}[/latex]

Discussion

Note that the imparted athwart momentum does not depend on any belongings of the object but only on torque and time. The final angular velocity is equivalent to one revolution in 8.71 s (determination of the time period is left as an practise for the reader), which is about right for a lazy Susan.

Example 3: Calculating the Torque in a Boot

The person whose leg is shown in Figure ii kicks his leg by exerting a 2000-Due north force with his upper leg muscle. The effective perpendicular lever arm is 2.twenty cm. Given the moment of inertia of the lower leg is [latex]{1.25\text{ kg}\cdotp\text{m}^2},[/latex] (a) detect the athwart acceleration of the leg. (b) Neglecting the gravitational force, what is the rotational kinetic energy of the leg after it has rotated through [latex]{57.iii^0}[/latex] (1.00 rad)?

Figure 2. The musculus in the upper leg gives the lower leg an angular dispatch and imparts rotational kinetic energy to it by exerting a torque about the knee. F is a vector that is perpendicular to r. This instance examines the situation.

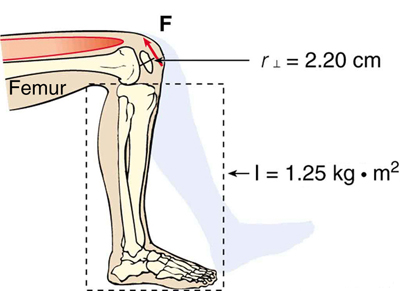
Strategy

The angular acceleration can be found using the rotational analog to Newton's second law, or [latex]{\alpha=\text{net }\tau/I}.[/latex] The moment of inertia [latex]{I}[/latex] is given and the torque tin be found easily from the given force and perpendicular lever arm. One time the angular acceleration [latex]{\blastoff}[/latex] is known, the final athwart velocity and rotational kinetic energy tin be calculated.

Solution to (a)

From the rotational analog to Newton's 2d law, the athwart acceleration [latex]{\alpha}[/latex] is

[latex]{\alpha=}[/latex] [latex]{\frac{\text{net}\;\tau}{{I}}}.[/latex]

Considering the force and the perpendicular lever arm are given and the leg is vertical and then that its weight does not create a torque, the net torque is thus

[latex]\begin{array}{lcl} {\text{net }\tau} & {=} & {r_{\perp}F} \\ {} & {=} & {(0.0220\text{ yard})(2000\text{ N})} \\ {} & {=} & {44.0\text{ N}\cdotp\text{m.}} \stop{assortment}[/latex]

Substituting this value for the torque and the given value for the moment of inertia into the expression for [latex]{\alpha}[/latex] gives

[latex]{\alpha\:=}[/latex] [latex]{\frac{44.0\text{ N}\cdotp\text{m}}{ane.25\text{ kg}\cdotp\text{one thousand}^2}}[/latex] [latex]{=\:35.two\text{ rad/s}^two}.[/latex]

Solution to (b)

The final angular velocity can be calculated from the kinematic expression

[latex]{\omega^ii=\omega_0^two+2\blastoff\theta}[/latex]

or

[latex]{\omega^2=two\alpha\theta}[/latex]

because the initial angular velocity is nada. The kinetic energy of rotation is

[latex]{\text{KE}_{\text{rot}}\:=}[/latex] [latex]{\frac{i}{2}}[/latex] [latex]{I\omega^ii}[/latex]

and so information technology is most convenient to utilise the value of [latex]{\omega^2}[/latex] just institute and the given value for the moment of inertia. The kinetic energy is then

[latex]\begin{array}{lcl} \text{KE}_{\text{rot}} & {=} & {0.5(1.25\text{ kg}\cdotp\text{1000}^2)(70.4\text{ rad}^2\text{/south}^2)} \\ {} & {=} & {44.0\text{ J.}} \end{array}[/latex]

Word

These values are reasonable for a person kicking his leg starting from the position shown. The weight of the leg can be neglected in part (a) considering information technology exerts no torque when the center of gravity of the lower leg is directly beneath the pivot in the human knee. In part (b), the forcefulness exerted past the upper leg is and then large that its torque is much greater than that created by the weight of the lower leg as it rotates. The rotational kinetic energy given to the lower leg is enough that information technology could give a ball a pregnant velocity by transferring some of this energy in a kick.

MAKING CONNECTIONS: CONSERVATION LAWS

Angular momentum, like free energy and linear momentum, is conserved. This universally applicable police is another sign of underlying unity in concrete laws. Angular momentum is conserved when net external torque is cipher, just equally linear momentum is conserved when the net external forcefulness is zilch.

We tin now understand why Earth keeps on spinning. As we saw in the previous instance, [latex]{\Delta{Fifty}=(\text{internet }\tau)\Delta{t}}.[/latex] This equation means that, to modify angular momentum, a torque must act over some period of time. Because World has a large angular momentum, a large torque acting over a long time is needed to change its rate of spin. And so what external torques are there? Tidal friction exerts torque that is slowing Earth's rotation, but tens of millions of years must pass earlier the modify is very meaning. Recent research indicates the length of the day was 18 h some 900 1000000 years ago. Only the tides exert significant retarding torques on Earth, and then it volition go along to spin, although ever more slowly, for many billions of years.

What we have here is, in fact, some other conservation constabulary. If the net torque is zero, then angular momentum is constant or conserved. We can see this rigorously by because [latex]{\text{net }\tau=\frac{\Delta{L}}{\Delta{t}}}[/latex] for the state of affairs in which the internet torque is zero. In that case,

[latex]{\text{net}\tau=0}[/latex]

implying that

[latex]{\frac{\Delta{L}}{\Delta{t}}}[/latex] [latex]{=0}.[/latex]

If the change in angular momentum [latex]{\Delta{Fifty}}[/latex] is zero, then the angular momentum is abiding; thus,

[latex]{L=\text{constant }(\text{internet }\tau=0)}[/latex]

or

[latex]{50=L^{\prime number}(\text{cyberspace }\tau=0).}[/latex]

These expressions are the law of conservation of angular momentum . Conservation laws are as scarce equally they are important.

An example of conservation of athwart momentum is seen in Figure three, in which an water ice skater is executing a spin. The internet torque on her is very shut to zero, because there is relatively little friction between her skates and the water ice and considering the friction is exerted very close to the pivot point. (Both [latex]{F}[/latex] and [latex]{r}[/latex] are small, and then [latex]{\tau}[/latex] is negligibly small.) Consequently, she can spin for quite some fourth dimension. She can do something else, too. She can increment her charge per unit of spin by pulling her arms and legs in. Why does pulling her arms and legs in increase her charge per unit of spin? The reply is that her athwart momentum is abiding, so that

[latex]{L=Fifty^{\prime}.}[/latex]

Expressing this equation in terms of the moment of inertia,

[latex]{I\omega=I^{\prime}\omega^{\prime},}[/latex]

where the primed quantities refer to weather condition after she has pulled in her arms and reduced her moment of inertia. Because [latex]{I^{\prime number}}[/latex] is smaller, the angular velocity [latex]{\omega^{\prime}}[/latex] must increase to keep the angular momentum constant. The change can be dramatic, as the post-obit case shows.

Effigy 3. (a) An ice skater is spinning on the tip of her skate with her arms extended. Her angular momentum is conserved considering the internet torque on her is negligibly small. In the next image, her rate of spin increases profoundly when she pulls in her arms, decreasing her moment of inertia. The work she does to pull in her artillery results in an increase in rotational kinetic energy.

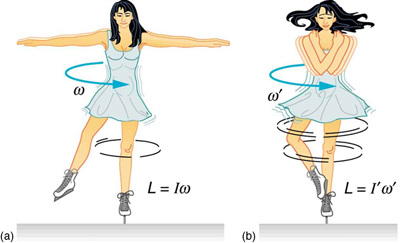
Example 4: Calculating the Angular Momentum of a Spinning Skater

Suppose an ice skater, such equally the one in Figure 3, is spinning at 0.800 rev/ s with her arms extended. She has a moment of inertia of [latex]{2.34\text{ kg}\cdotp\text{m}^two}[/latex] with her artillery extended and of [latex]{0.363\text{ kg}\cdotp\text{yard}^2}[/latex] with her arms close to her body. (These moments of inertia are based on reasonable assumptions well-nigh a 60.0-kg skater.) (a) What is her angular velocity in revolutions per 2d afterward she pulls in her arms? (b) What is her rotational kinetic energy before and after she does this?

Strategy

In the starting time part of the problem, we are looking for the skater's angular velocity [latex]{\omega^{\prime}}[/latex] after she has pulled in her arms. To find this quantity, we utilise the conservation of angular momentum and note that the moments of inertia and initial athwart velocity are given. To find the initial and final kinetic energies, nosotros use the definition of rotational kinetic energy given by

[latex]{\text{KE}_{\text{rot}}\:=}[/latex] [latex]{\frac{1}{ii}}[/latex] [latex]{I\omega^2.}[/latex]

Solution for (a)

Because torque is negligible (as discussed above), the conservation of angular momentum given in [latex]{I\omega=I^{\prime}\omega^{\prime number}}[/latex] is applicable. Thus,

[latex]{L=Fifty^{\prime}}[/latex]

or

[latex]{I\omega=I^{\prime}\omega^{\prime number}}[/latex]

Solving for [latex]{\omega^{\prime}}[/latex] and substituting known values into the resulting equation gives

[latex]\begin{array}{lcl} {\omega^{\prime}} & {=} & {\frac{I}{I^{\prime}}\omega=(\frac{two.34\text{ kg}\cdotp\text{grand}^two}{0.363\text{ kg}\cdotp\text{grand}^2})(0.800\text{ rev/s})} \\ {} & {=} & {v.16\text{ rev/s.}} \end{array}[/latex]

Solution for (b)

Rotational kinetic free energy is given by

[latex]{\text{KE}_{\text{rot}}\:=}[/latex] [latex]{\frac{one}{2}}[/latex] [latex]{I\omega^two.}[/latex]

The initial value is found by substituting known values into the equation and converting the angular velocity to rad/southward:

[latex]\brainstorm{assortment}{lcl} \text{KE}_{\text{rot}} & {=} & {(0.5)(2.34\text{ kg}\cdotp\text{m}^two)((0.800\text{ rev/s})(2\pi\text{ rad/rev}))^2} \\ {} & {=} & {29.6\text{ J.}} \stop{array}[/latex]

The last rotational kinetic energy is

[latex]{\text{KE}_{\text{rot}}^{\prime}\:=}[/latex] [latex]{\frac{1}{2}}[/latex] [latex]{I^{\prime}{\omega}^{\prime{two}}}[/latex]

Substituting known values into this equation gives

[latex]\begin{assortment}{lcl} {\text{KE}_{\text{rot}}^{\prime}} & {=} & {(0.5)(0.363\text{ kg}\cdotp\text{m}^2)[(5.16\text{ rev/s})(2\pi\text{ rad/rev})]^ii} \\ {} & {=} & {191\text{ J.}} \finish{array}[/latex]

Discussion

In both parts, in that location is an impressive increase. Outset, the terminal angular velocity is large, although about globe-class skaters can attain spin rates about this great. Second, the terminal kinetic energy is much greater than the initial kinetic energy. The increment in rotational kinetic energy comes from work done by the skater in pulling in her artillery. This work is internal work that depletes some of the skater's food energy.

There are several other examples of objects that increase their charge per unit of spin considering something reduced their moment of inertia. Tornadoes are 1 instance. Storm systems that create tornadoes are slowly rotating. When the radius of rotation narrows, fifty-fifty in a local region, athwart velocity increases, sometimes to the furious level of a tornado. Globe is another example. Our planet was born from a huge cloud of gas and grit, the rotation of which came from turbulence in an even larger deject. Gravitational forces caused the cloud to contract, and the rotation charge per unit increased as a result. (See Effigy 4.)

Effigy four. The Solar System coalesced from a cloud of gas and dust that was originally rotating. The orbital motions and spins of the planets are in the aforementioned direction as the original spin and conserve the athwart momentum of the parent cloud.

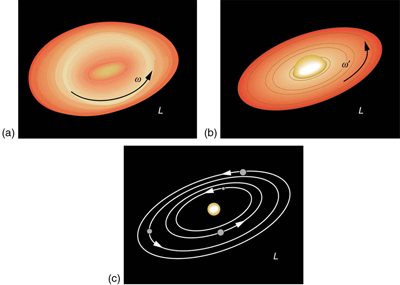
In case of man movement, one would non expect athwart momentum to be conserved when a body interacts with the environment as its human foot pushes off the basis. Astronauts floating in space aboard the International Space Station have no angular momentum relative to the within of the ship if they are motionless. Their bodies volition go on to have this cypher value no matter how they twist virtually as long as they exercise not give themselves a push off the side of the vessel.

Check Your Understanding

1: Is angular momentum completely analogous to linear momentum? What, if any, are their differences?

• Every rotational miracle has a direct translational analog , likewise angular momentum [latex]{L}[/latex] tin can be defined as [latex]{Fifty=I\omega}.[/latex]
• This equation is an analog to the definition of linear momentum equally [latex]{p=mv}.[/latex] The relationship between torque and angular momentum is [latex]{\text{net }\tau=\frac{\Delta{L}}{\Delta{t}}}.[/latex]
• Angular momentum, similar energy and linear momentum, is conserved. This universally applicable law is another sign of underlying unity in physical laws. Athwart momentum is conserved when cyberspace external torque is nix, merely as linear momentum is conserved when the cyberspace external force is zero.

Conceptual Questions

1: When you start the engine of your automobile with the transmission in neutral, y'all notice that the auto rocks in the reverse sense of the engine's rotation. Explain in terms of conservation of angular momentum. Is the angular momentum of the motorcar conserved for long (for more than a few seconds)?

ii: Suppose a child walks from the outer border of a rotating merry-go circular to the inside. Does the angular velocity of the merry-go-circular increase, decrease, or remain the same? Explain your answer.

Effigy 5. A kid may jump off a merry-go-round in a variety of directions.

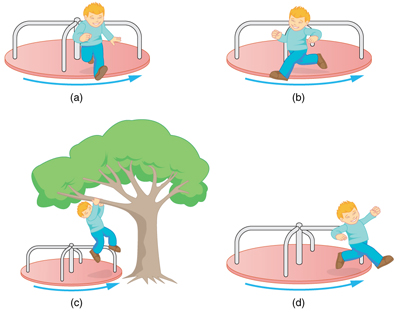
three: Suppose a kid gets off a rotating merry-become-round. Does the athwart velocity of the merry-go-circular increase, decrease, or remain the aforementioned if: (a) He jumps off radially? (b) He jumps astern to land motionless? (c) He jumps directly up and hangs onto an overhead tree co-operative? (d) He jumps off forwards, tangential to the edge? Explicate your answers. (Refer to Figure 5).

4: Helicopters take a pocket-sized propeller on their tail to proceed them from rotating in the opposite direction of their chief lifting blades. Explain in terms of Newton'south third law why the helicopter body rotates in the contrary direction to the blades.

5: Whenever a helicopter has ii sets of lifting blades, they rotate in opposite directions (and there will be no tail propeller). Explain why it is all-time to have the blades rotate in opposite directions.

6: Depict how work is done by a skater pulling in her arms during a spin. In item, identify the force she exerts on each arm to pull information technology in and the distance each moves, noting that a component of the force is in the direction moved. Why is athwart momentum not increased by this action?

7: When there is a global heating tendency on Globe, the atmosphere expands and the length of the day increases very slightly. Explain why the length of a 24-hour interval increases.

viii: Nearly all conventional piston engines have flywheels on them to smooth out engine vibrations caused by the thrust of individual piston firings. Why does the flywheel have this effect?

nine: Jet turbines spin rapidly. They are designed to fly apart if something makes them seize of a sudden, rather than transfer angular momentum to the aeroplane'southward fly, possibly tearing it off. Explain how flight apart conserves angular momentum without transferring it to the fly.

10: An astronaut tightens a bolt on a satellite in orbit. He rotates in a direction opposite to that of the commodities, and the satellite rotates in the same direction as the bolt. Explain why. If a handhold is available on the satellite, can this counter-rotation be prevented? Explain your answer.

11: Competitive divers pull their limbs in and curl up their bodies when they exercise flips. Just before entering the water, they fully extend their limbs to enter straight down. Explain the event of both deportment on their angular velocities. Also explain the event on their angular momenta.

Figure 6. The diver spins rapidly when curled upwards and slows when she extends her limbs before inbound the h2o.

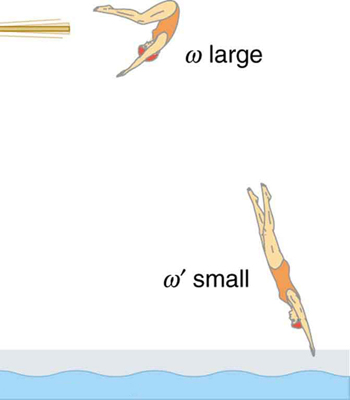
12: Depict a free body diagram to show how a diver gains angular momentum when leaving the diving board.

13: In terms of angular momentum, what is the advantage of giving a football or a rifle bullet a spin when throwing or releasing information technology?

Figure vii. The image shows a view downward the butt of a cannon, emphasizing its rifling. Rifling in the barrel of a canon causes the projectile to spin simply every bit is the case for rifles (hence the name for the grooves in the butt). (credit: Elsie esq., Flickr)

Problems & Exercises

1: (a) Calculate the angular momentum of the Earth in its orbit around the Lord's day.

(b) Compare this angular momentum with the angular momentum of Globe on its axis.

two: (a) What is the angular momentum of the Moon in its orbit around Globe?

(b) How does this angular momentum compare with the athwart momentum of the Moon on its centrality? Retrieve that the Moon keeps one side toward Earth at all times.

(c) Talk over whether the values plant in parts (a) and (b) seem consistent with the fact that tidal effects with Earth take acquired the Moon to rotate with one side always facing Earth.

3: Suppose you offset an antique auto by exerting a strength of 300 Due north on its crank for 0.250 due south. What angular momentum is given to the engine if the handle of the creepo is 0.300 m from the pivot and the force is exerted to create maximum torque the entire time?

iv: A playground merry-go-round has a mass of 120 kg and a radius of ane.lxxx m and it is rotating with an angular velocity of 0.500 rev/s. What is its angular velocity later a 22.0-kg child gets onto it by grabbing its outer edge? The child is initially at rest.

5: Three children are riding on the edge of a merry-go-round that is 100 kg, has a i.60-m radius, and is spinning at 20.0 rpm. The children have masses of 22.0, 28.0, and 33.0 kg. If the child who has a mass of 28.0 kg moves to the center of the merry-go-circular, what is the new angular velocity in rpm?

6: (a) Calculate the angular momentum of an ice skater spinning at vi.00 rev/southward given his moment of inertia is [latex]{0.400\text{ kg}\cdotp\text{thousand}^two}.[/latex] (b) He reduces his rate of spin (his angular velocity) by extending his arms and increasing his moment of inertia. Find the value of his moment of inertia if his athwart velocity decreases to 1.25 rev/due south. (c) Suppose instead he keeps his arms in and allows friction of the ice to slow him to 3.00 rev/s. What average torque was exerted if this takes 15.0 due south?

7:  Construct Your Own Problem

Consider the World-Moon organization. Construct a problem in which y'all calculate the full athwart momentum of the arrangement including the spins of the Earth and the Moon on their axes and the orbital angular momentum of the Earth-Moon arrangement in its well-nigh monthly rotation. Summate what happens to the Moon'due south orbital radius if the Earth'due south rotation decreases due to tidal drag. Among the things to be considered are the amount by which the Earth's rotation slows and the fact that the Moon will go along to have 1 side always facing the Globe.

Glossary

angular momentum

the product of moment of inertia and athwart velocity

constabulary of conservation of angular momentum

angular momentum is conserved, i.e., the initial athwart momentum is equal to the concluding angular momentum when no external torque is applied to the arrangement

Solutions

Check Your Agreement

1: Yes, angular and linear momentums are completely analogous. While they are exact analogs they have different units and are not directly inter-convertible like forms of free energy are.

Problems & Exercises

1:

(a) [latex]{2.66\times10^{40}\text{ kg}\cdotp\text{m}^two\text{/s}}[/latex]

(b) [latex]{7.07\times10^{33}\text{ kg}\cdotp\text{k}^2\text{/s}}[/latex]

The angular momentum of the World in its orbit around the Sunday is [latex]{three.77\times10^6}[/latex] times larger than the angular momentum of the Earth around its centrality.

3:

[latex]{22.5\text{ kg}\cdotp\text{m}^2\text{/s}}[/latex]

5:

25.3 rpm

rotherbehienceeten51.blogspot.com

Source: https://pressbooks.online.ucf.edu/algphysics/chapter/angular-momentum-and-its-conservation/

Share this post